A simple house rule idea that just occurred to me, for D&D and similar games: damage from a successful attack = 1 + attack roll degree of success. The 1 is necessary so that some damage is still done when the attack roll succeeds exactly (otherwise, you are essentially applying a -1 penalty to the attack roll).
Some benefits:
- One roll rather than two.
- Makes clear the true nature of the attack roll (expected damage is the important thing).
- Higher level fighters do increasing damage in a pleasing way.
- The attack roll has many seeming degrees of success.
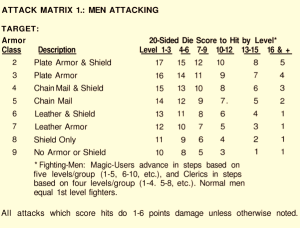
Expected damage numbers are provided below, for fighters of levels 1, 4, 7, and 10 against ACs of 9 and 2 using ATTACK MATRIX 1 from Men & Magic, page 19 (B/X uses identical numbers other than for zero level people; see the Expert Rules page X26). These numbers are averaged over all die possibilities, including misses, and so are expected damage per round. Comparisons with expected numbers from weapons dealing 1d6 (average: 3.5) damage are provided in parentheses.
| Fighter Level | Damage Versus AC 9 | Damage Versus AC 2 |
|---|---|---|
| 1 | 3.3 (1.925) | 0.5 (0.7) |
| 4 | 4.55 (2.275) | 1.05 (1.05) |
| 7 | 6.8 (2.8) | 3.3 (1.925) |
| 10 | 8.55 (3.15) | 4.55 (2.275) |
You will see that in general, this shifts the damage potential up for most situations (all, in fact, other than first level versus AC 2, at least of those data points shown in the table). ACs 9 and 2 were chosen because they encompasses the full OD&D range from unarmored to plate & shield. Results are independent of other bonuses, which will just raise or lower the expected numbers for all schemes. I imagine the numbers would remain somewhat similar if using a simplification such as hit dice as attack bonus. The same numbers obtain for the other classes, though the level ranges are different (a 9th level cleric hits as a 7th level fighter, for example).
The expected values are close enough that this adjustment will obviously not break the game, though it might shift the dynamics slightly. One could also cap damage at 6 for slightly more restrained damage results (just for comparison, with that modification numbers versus AC 9 become: 2.55, 3.15, 4.05, 4.65 for levels 1, 4, 7, 10 respectively and have a much smaller standard deviation).
The spreadsheets that I used to calculate these numbers can be found here: