Landscape by Nicholas Roerich (source)
Starting from the idea of distance may not be the most productive way to approach either running or mapping the wilderness. This is counterintuitive, because measurement and mapping are so tightly linked conceptually. However, a graph of locations with adjacency (sometimes called a point-crawl recently) seems like too much abstraction. As an attempt to navigate between these two extremes, consider the following system, which I have been using in my Vaults of Pahvelorn game.
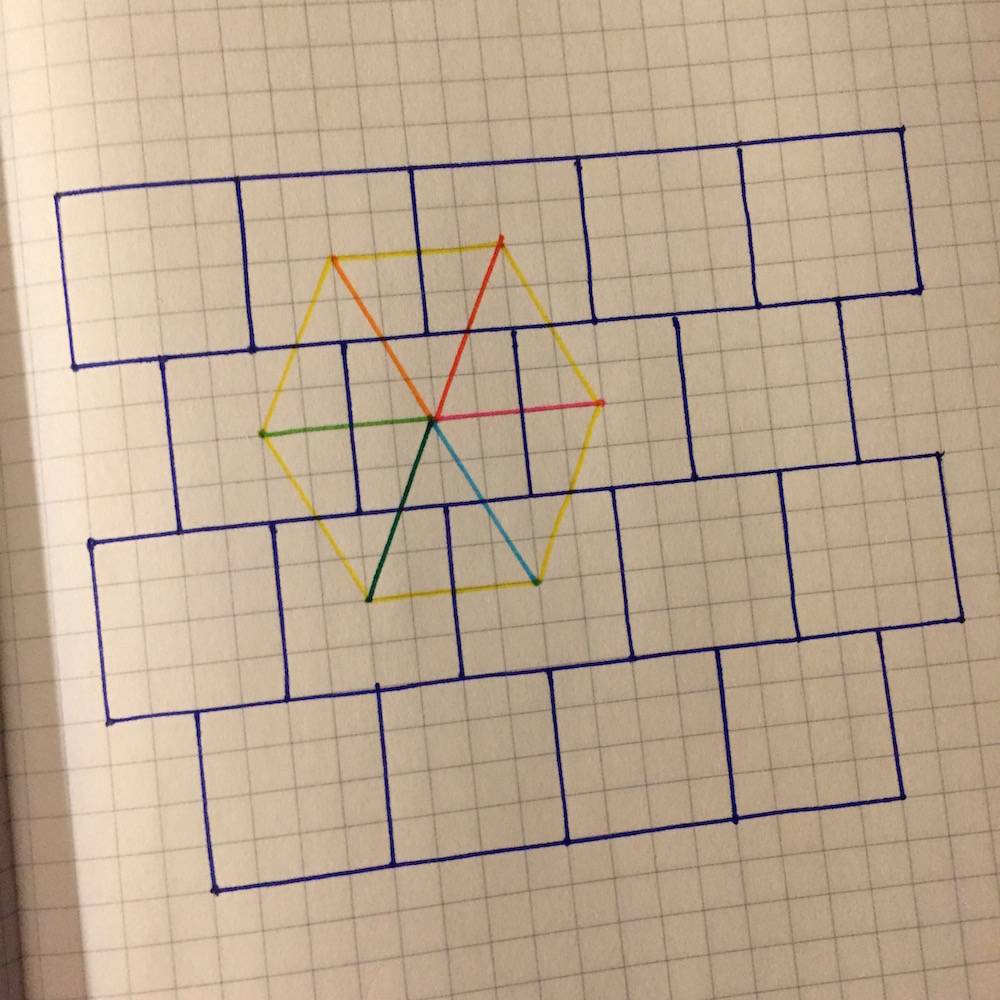
Hexes don’t have any determinate size at all. They are abstractions built around three things: sites, travel time, and landmarks. Sites are the locations (towns, dungeons, towers, ancient battlefields, etc) within a hex that can be visited. Sites are either obvious or hidden. One day of travel allows visiting any obvious site within the current hex or within an adjacent hex (this is “moving through hexes” mode). A day may also be spent to search the current hex (which provides a chance of finding a hidden site). Or, to rephrase it in more game-oriented terms, players get one “move” per wilderness turn, which can either be moving to an obvious location within one step or searching the current hex for hidden locations.
Travel time is probably the most controversial aspect of this scheme. One day per hex, irrespective of anything else. Travelling to an adjacent hex allows characters to interact with any of the obvious features of that hex (such as stopping in a town). Exploring a hex provides a 1 in 6 chance to find one of the hidden sites. Any site found is determined randomly, unless the characters are looking for something specific, in which case chance might be weighted in that direction based on if the characters know something about the location they are looking for (“the tomb is by a stream”). A hidden site is treated as obvious if a knowledgeable guide or accurate map is available. The relative locations of sites within a hex are usually not important, and are determined randomly or arbitrarily as needed.
Landmarks, in addition to large obvious features of the current hex, include large obvious features of adjacent hexes. This provides players with information so that they can make meaningful choices about where to go. Most of the time, characters should be able to tell the basic terrain type of all adjacent hexes, though occasionally local terrain will prevent this (such as wandering at the bottom of canyons, or journeying through a very dense forest). This should be clear by context, and limitations are often easy to overcome (such as by climbing a tree).
Each day spent in the wilderness necessitates a random encounter check, as does each night. This is a 1 in 6 chance, but can be adjusted per-hex (based on terrain type or general danger level). It is perfectly functional to stick with the 1 in 6 chance in general, for simplicity’s sake. If an encounter is indicated, I sometimes roll another d6 to see if more than one encounter might occur (a 6 on the second die) or if the encounter will involve more than one NPC group (a 1 on the second die). In the second case, “more than one NPC group” means that the PCs encounter two other groups that are already engaged in an encounter themselves. The exact probabilities for the rarer occurrences are not important as long as they are impartially determined and remain uncommon.
Exploring off the beaten path carries with it the risk of getting lost. There is no chance of getting lost when following a known route, such as a road, but in other cases the chance is 1 in 6 (or greater, of course, depending on the situation and terrain). In game terms, getting lost means wandering accidentally into a hex adjacent to the one intended (determine which randomly). This can happen either during movement toward a known site (if a path is not followed) or during searching for hidden sites.
By implication, the “real” size (whatever that might mean) of a predominantly mountain hex is smaller that the size of a plains hex (because you can travel much farther on plains than on mountains). What this does is pull the wilderness into a loose mesh similar to a point-crawl, but with more enforced structure (as there will always be six adjacent nodes at any given location).
Just like in the dungeon, the default rate of travel assumes caution, resting occasionally, and so forth. Journeys are purposeful but not forced marches. This mode engages all the standard rules (mounts not dying on you, standard getting lost chances, standard encounter chances, standard surprise chances, standard encounter distances). If a group wants to throw caution to the wind and make like a bat out of hell to their destination, more than one hex may be traversed in a single day of travel, but chances of mishap are be greater. Roll or pick any number of possibilities from the following list:
- One encounter check (with increased chance) per hex traversed
- Mounts must save or die when destination is reached
- Increased chance of getting lost (if appropriate)
- Guaranteed attention from bandits (haste implies value)
- Guaranteed pursuit from origin location (haste attracts attention)
- Force retainer morale check (“I didn’t sign up for this garbage”)
- Otherwise obvious landmarks or sites go unnoticed
- Increased chance of being surprised during encounters
- Decreased encounter distance
- Penalty to encounter reaction rolls
Alex S. uses a similar one day per hex method, and his post helped lead me to my current method, though I do not expose hexes directly to players.
Current hexcrawl procedure:
- Roll for weather (2d6 reaction roll with cosmos)
- Move or search?
- Day encounter check
- Lost?
- Describe travel, note obvious sites and landmarks
- Resolve any day encounters
- Camp procedures? (establishing “default” procedures is reasonable)
- Mark off rations (I always forget to do this — bad referee!)
- Night encounter check
- Resolve nocturnal encounters